
Discussione
del problema
Per risolvere il
problema posto utilizziamo il principio di conservazione dell’energia
meccanica.
Assumiamo
come riferimento zero per l’energia potenziale gravitazionale quella del piano
orizzontale passante per la posizione occupata dal centro O quando
questo raggiunge la quota più in basso. Inizialmente
il disco è fermo, quindi è in possesso della sola energia potenziale
gravitazionale data da Ui=MgR.
Una
volta libero di ruotare il disco descrive un moto rotatorio intorno all’asse
perpendicolare al suo piano passante per il punto A e la sua energia meccanica,
puramente rotazionale, è
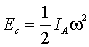 , dove IA
è il momento d’inerzia rispetto al suddetto asse di rotazione ed w
il modulo della velocità angolare rispetto allo stesso asse. Indicando con VO
il modulo della velocità lineare del centro del disco si ha VO=wR;
inoltre
per il teorema di Steiner il momento IA
risulta
, dove IA
è il momento d’inerzia rispetto al suddetto asse di rotazione ed w
il modulo della velocità angolare rispetto allo stesso asse. Indicando con VO
il modulo della velocità lineare del centro del disco si ha VO=wR;
inoltre
per il teorema di Steiner il momento IA
risulta
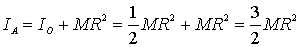 .
.
Per
l’energia cinetica si può scrivere:
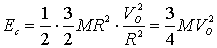
Per
la conservazione dell’energia questo valor deve uguagliare l’energia
iniziale disponibile, quindi
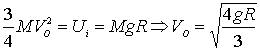
Per quanto
riguarda la velocità del punto B possiamo affermare che risulta doppia di
quella del centro O in quanto si ha
VB=2Rw=2VO e quindi
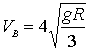
torna su