Sistema
di particelle
Consideriamo
un sistema di particelle puntiformi di
masse m1,m2,m3,
,mN che nello spazio occupano le posizioni P1,P2,P3,….,PN
. Sussiste la seguente
Definizione
Si chiama centro di massa del
sistema di particelle il punto G dello spazio che verifica la seguente
equazione vettoriale
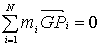 (1)
(1)
Vogliamo
dimostrare che per qualunque sistema di particelle esiste sempre un solo
punto G nello spazio che verifica la (1).
Infatti,
detto O l’origine del sistema di riferimento di assi cartesiani
ortogonali adottato ricordiamo che per la definizione di somma di due
vettori , per ogni punto Pi occupato dalla particella i-esima ,
si può scrivere:
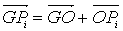 (1.1)
(1.1)
L’equazione
(1) può essere allora posta nella forma
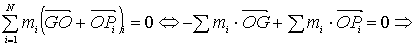
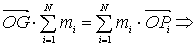
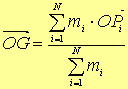 (1.3)
(1.3)
La
(1.3) indica operativamente come procedere per determinare la posizione
del centro di massa G costruendo il suo vettore di posizione
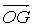 . Dunque per ogni sistema di particelle esiste il punto G ed è unico.
. Dunque per ogni sistema di particelle esiste il punto G ed è unico.
Proiettando
la (1.3) sugli assi coordinati si ricavano le espressioni delle coordinate
del centro di massa.
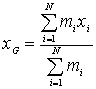 ,
,
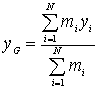 ,
,
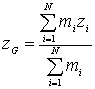
Si noti
che in base alla definizione data, e lo si intuisce anche dalle coordinate
ottenute, il centro di massa di un sistema di particelle non coincide in
genere con uno dei punti delle particelle elementari, ma è un punto dello
spazio che comunque esiste.
torna
su
Corpo
rigido continuo esteso
Per
un corpo continuo di massa M si
definisce ugualmente il centro di massa ed il vettore posizione che lo
individua è
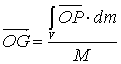 (2)
(2)
Si
tratta di un integrale di volume perché deve essere eseguito su tutto il
volume occupato dal corpo ; dm
indica la massa elementare ed
OP
il suo vettore posizione .
Se
il corpo non è omogeneo è necessario conoscere come varia la sua densità
r(x;y;z); in tal caso la (2) diventa
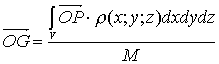 (3)
(3)
Scriviamo della (2) le espressioni scalari che
forniscono le tre coordinate del punto G.
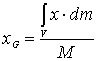 ;
;
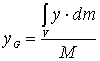 ;
;
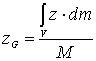
torna su