Dimostrazione
Consideriamo
un piano ao
passante per il centro della sfera e perpendicolare all’asse a.
Per dedurre la formula è necessario pensare al guscio sferico come composto da
tante parti elementari di ciascuna delle quali si sa trovare il momento
d’inerzia rispetto all’asse prefissato. La parte elementare che vogliamo
considerare è il sottile anello
 del guscio sferico compreso tra due
piani a1
, a2
paralleli al piano ao
e molto vicini tra loro. In
figura è rappresentato un tale anello. Intersecando questo anello con il piano b
passante per il suo centro e perpendicolare al piano dell’anello stesso (si
pensi al piano del foglio), che contiene l’asse a, si
ottengono due archi di circonferenza di lunghezza dl.
Detto P un punto dell’anello appartenente ad uno dei suddetti archi elementari,
P’ la sua proiezione ortogonale sul piano ao,
O il centro della sfera, l’angolo
del guscio sferico compreso tra due
piani a1
, a2
paralleli al piano ao
e molto vicini tra loro. In
figura è rappresentato un tale anello. Intersecando questo anello con il piano b
passante per il suo centro e perpendicolare al piano dell’anello stesso (si
pensi al piano del foglio), che contiene l’asse a, si
ottengono due archi di circonferenza di lunghezza dl.
Detto P un punto dell’anello appartenente ad uno dei suddetti archi elementari,
P’ la sua proiezione ortogonale sul piano ao,
O il centro della sfera, l’angolo
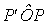 misura q . Ebbene, unendo con il centro O gli estremi
di uno degli archi dell’anello intercettati sul piano b si determina un angolo di ampiezza dq e la misura dl dell’arco in
oggetto è
misura q . Ebbene, unendo con il centro O gli estremi
di uno degli archi dell’anello intercettati sul piano b si determina un angolo di ampiezza dq e la misura dl dell’arco in
oggetto è
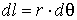 .
.
Avendo
considerato i piani a1
,
a2
molto vicini tra
loro possiamo ritenere la superficie dell’anello come quella del cilindro
circolare retto di raggio OP’ ed
altezza dl e
scrivere quindi il valore della sua area come segue
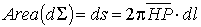 (G.2)
(G.2)
Introduciamo
ora il concetto di
Densità superficiale
di massa
Definiamo densità superficiale di massa per
il guscio sferico omogeneo di massa M e raggio r
il rapporto tra la massa del guscio e l’area della superficie sferica. Quindi
 (G.3)
(G.3)
La
massa dm concentrata nell’anello
 è
è
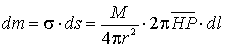
Notiamo
ora che

e
dunque possiamo scrivere il momento d’inerzia della massa dm
rispetto all’asse a giacché si tratta
di applicare la legge del momento d’inerzia di un anello omogeneo di raggio HP
rispetto all’asse baricentrale perpendicolare al piano dell’anello. Dunque
risulta:
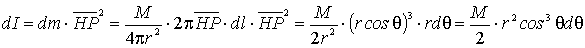
Ora per
calcolare il momento d’inerzia del guscio sferico è sufficiente eseguire il
calcolo dell’integrale definito sulla variabile q
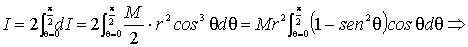
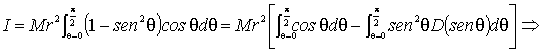
 .
C.V.D.
.
C.V.D.
torna su