
Discussione del problema
1) Il problema si risolve applicando i principi
di conservazione dell’energia e del momento angolare.
Infatti nella caduta la barretta ed il corpo C1 perdono
energia gravitazionale perché si abbassano le quote dei loro centri di massa.
Precisamente, il centro di massa della barretta scende di L/2 e quello del corpo
C1 scende della misura L. Quest’energia si trasforma interamente in
energia di rotazione dei due corpi e quindi, indicando:
·
con
w
il modulo della velocità angolare posseduta dalla barretta e dal corpo C1
subito prima dell’urto;
·
con ICM
il momento d’inerzia della barretta rispetto all’asse baricentrale parallelo
all’asse di rotazione, che ricordiamo vale
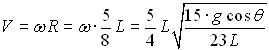 ;
;
·
con IA
il momento d’inerzia della barretta calcolato rispetto all’asse di
rotazione, dal teorema di Steiner si deduce il momento IA :
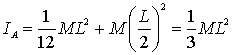
Poiché
per un corpo in rotazione con velocità angolare w
intorno ad un asse rispetto al quale il momento d’inerzia sia I, l’energia
meccanica di rotazione è data da
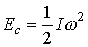
per
l’energia di rotazione della barretta e del corpo C1
subito prima dell’urto possiamo scrivere la seguente espressione
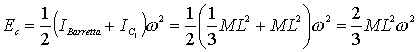
Dicevamo che quest’energia è uguale all’energia
gravitazionale persa complessivamente dalla barretta e dal corpo C1,
che è:
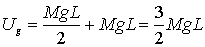 (1.1)
(1.1)
Uguagliando le due espressioni si determina il valore
della velocità angolare:
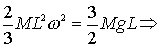
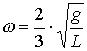
torna
su

2) L’urto è elastico e quindi si conservano l’energia
meccanica ed il momento angolare del sistema composto dalla barretta e dai due
corpi C1, C2.
Indichiamo:
con
V2 il modulo
della velocità lineare con cui parte il corpo C2 subito dopo
l’urto;
con
w1 il modulo della velocità angolare della barretta e del
corpo C1 dopo l’urto rispetto all’asse di rotazione.
Ricordiamo
che il momento angolare di un corpo che ruota rispetto ad un asse è dato da Iw,
essendo I il momento d’inerzia rispetto
all’asse di rotazione. Per il principio di conservazione del momento angolare
(il sistema dei tre corpi è isolato) possiamo uguagliare il valore del momento
angolare del sistema prima dell’urto, dato dal momento angolare della barretta
e del corpo C1, al valore del momento angolare del sistema meccanico
dopo l’urto. Dopo l’urto il momento angolare è dato dalla somma del momento
angolare della barretta, da quello del corpo C1 e da quello del corpo
C2 .Il momento angolare di quest’ultimo vale
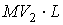 .
.
Il
momento angolare della barretta e del corpo C1 dopo l’urto è:
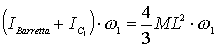 ;
;
il momento angolare prima dell’urto è
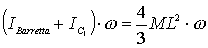 .
.
Sussiste allora l’uguaglianza
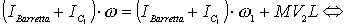
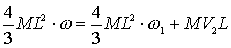 (2.1)
(2.1)
Il
principio di conservazione dell’energia meccanica nell’urto permette di
ricavare una seconda equazione uguagliando l’energia cinetica prima
dell’urto data dall’energia di rotazione della barretta caricata,
all’energia cinetica dopo l’urto data dalla somma dell’energia cinetica
della barretta caricata con l’energia cinetica acquistata dal corpo C2.
L’equazione è:
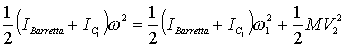
che deve essere soddisfatta dalle incognite w1
e V2 . Sostituendo i valori noti
delle grandezze otteniamo:
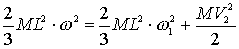 (2.2)
(2.2)
Risolvendo
il sistema composto dalle due equazioni (2.1), (2.2) si determinano i valori
della velocità angolare w1
e della velocità lineare del corpo C2. Riportiamo i loro valori
senza eseguire i calcoli algebrici.
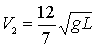 ,
,
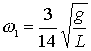

torna
su