
Sia P un punto
dell’anello e consideriamo un arco elementare centrato in P.
Indichiamo con dl
e dm rispettivamente la lunghezza dell’arco e la massa
elementare in esso concentrata. Detto O il centro dell’anello,
assumiamo la semiretta OA come origine per la misura dell’angolo
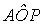 . Sia ancora H la proiezione ortogonale di P sulla semiretta OA.
. Sia ancora H la proiezione ortogonale di P sulla semiretta OA.
Alla
lunghezza dl dell’arco di
anello corrisponde l’angolo al centro di ampiezza dq
e sussiste la relazione
 (a.3)
(a.3)
tra
lunghezza dell’arco, raggio ed angolo al centro, ed in virtù della
definizione di densità lineare anche la relazione
 .
(a.4)
.
(a.4)
Per calcolare il momento d’inerzia della massa dm
rispetto all’asse a occorre
trovare la distanza da questo del punto P in cui supponiamo concentrata la
massa dm.
Poiché si ha evidentemente
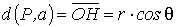 ,
,
per il
momento d’inerzia della massa dm,
possiamo scrivere l’espressione
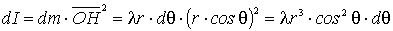
Osserviamo
ora che il momento d’inerzia della quarta parte dell’anello compresa
tra i punti A e B (vedi figura) è data dall’integrale definito
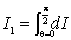
e che per ovvii motivi di simmetria il momento d’inerzia complessivo
dell’anello è
4I1. Si ha pertanto:
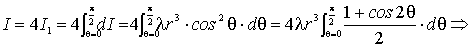
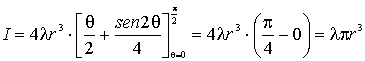
Possiamo dare un’altra forma al risultato trovato eliminando il
simbolo l della densità lineare e facendo invece
comparire la massa dell’anello.
Dalla (a.1) ricaviamo
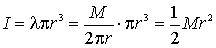
che è appunto la formula cercata.