|
|
Barretta in
un piano orizzontale
|
La
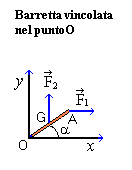
barretta si trova in un piano orizzontale, è vincolata nel suo estremo O
ed è sollecitata dalle forze F1,
F2; il vincolo esercita una
reazione vincolare R (non rappresentata) come indicato in
figura. La posizione di equilibrio dipende dalle intensità delle forze e
risulta univocamente determinata dall'ampiezza dell'angolo
a:
 |
 |
Problema (barretta vincolata)
Una barretta omogenea si trova su un piano orizzontale ed è vincolata a ruotare intorno al un suo estremo (il punto O in figura). Alla sua estremità libera A è applicata la forza F1 e nel suo baricentro G la forza F2 come in figura. La direzione della barretta forma un angolo acuto a con il semiasse positivo delle ascisse.
Determinare l’ampiezza dell’angolo a per il quale le due forze F1 , F2, insieme alla forza R vincolare esercitata dal perno O si fanno equilibrio. Determinare anche la reazione vincolare R.
Soluzione
La prima condizione per l’equilibrio richiede che la somma d elle forze agenti sulla barretta sia nulla. Detta R la reazione vincolare deve essere
R +F1 + F2 = 0 Þ R =-F1 - F2 (1)
La seconda condizione per l’equilibrio richiede che sia nullo il momento risultante di tutte le forze agenti calcolato rispetto ad un punto qualsiasi. Questa condizione equivale a richiedere che la barretta non ruoti rispetto ad alcun punto.
Scegliamo il centro di rotazione O come punto rispetto al quale calcolare il momento.
Notiamo che rispetto ad O il momento della reazione vincolare R è nullo, per cui il momento complessivo delle forze è
![]() ,
(2)
,
(2)
dove G indica il baricentro della barretta.
Indicando brevemente con l la lunghezza della barretta possiamo esprimere i vettori OA, OG nella forma cartesiana:
![]()
![]()
Determiniamo ora l’espressione cartesiana del momento totale ed imponiamo che si annulli.



Esempio
Nel caso particolare in cui F1 = 2,5N , F2 = 4N si ha

La reazione vincolare R =-F1 - F2 ha modulo
![]()
e forma con il semiasse positivo delle ascisse l’angolo b=122°0’19”.
|
|