Barretta ruota in un piano orizzontale intorno ad un estremo 

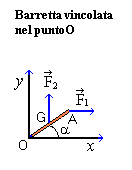
Problema - Una barretta su un piano orizzontale, vincolata in nell'estremo O e sottoposta a due forze. Il problema consiste determinare l’ampiezza dell’angolo a per il quale le due forze F₁ , F₂ , insieme alla forza R (non rappresentata in figura) vincolare esercitata dal perno O si fanno equilibrio
Vai alla soluzione del  problema

Problema - Un ciclista percorre una strada larga 8 metri procedendo lungo la linea mediana alla velocità di 28,8Km/h. Un osservatore è sul ciglio della strada ed osserva il moto. Sapendo che la massa del ciclista è di 60 Kg determinare:
1.1)  Il momento angolare del ciclista rispetto all’osservatore nell’istante in cui gli passa davanti ( Posizione P₁).
1.2)  Le componenti cartesiane del vettore posizione del ciclista rispetto all’osservatore nel momento in cui il ciclista si trova ad 8m di distanza da O (Posizione P₂). Considerare il ciclista come puntiforme.
1.3)   Determinare l’espressione vettoriale del momento angolare del ciclista rispetto all’osservatore quando è nella posizione P₂ servendosi del riferimento cartesiano ortogonale illustrato nella figura ed assumendo come terzo asse cartesiano quello perpendicolare al piano del foglio ed uscente da questo.
1.4)  Indicare come si esegue analiticamente l’operazione di prodotto vettoriale tra il vettore posizione OP₂ ed il vettore quantità di moto del ciclista nella posizione P₂.
1.5)  Siano A,B,C,D quattro successive posizioni occupate dal ciclista rispettivamente negli istanti t_A, t_B, t_C, t_D . Nell’ipotesi che gli intervalli di tempo [t_A; t_B], [t_C; t_D] abbiano la stessa durata , determinare le aree dei triangoli OAB, OCD, essendo O la posizione dell’osservatore ( origine di riferimento degli assi cartesiani). 
Vai alla soluzione del problema