|
| |
| Un ciclista si
muove su una strada rettilinea a velocità costante. Nel problema si
applica il concetto di prodotto vettoriale e si riconosce che si mantiene
costante il momento angolare del ciclista. |
|
Problema
Un
ciclista percorre una strada larga 8 metri procedendo lungo la linea mediana
alla velocità di 28,8Km/h. Un osservatore è sul ciglio della strada ed osserva
il moto. Sapendo che la massa del ciclista è di 60 Kg determinare:
1.1)
Il momento angolare del ciclista rispetto all’osservatore
nell’istante in cui gli passa davanti ( Posizione
P1).
1.2)
Le componenti cartesiane del vettore posizione del ciclista rispetto
all’osservatore nel momento in cui il ciclista si trova ad 8m di distanza da O
(Posizione P2). Considerare il
ciclista come puntiforme.
1.3)
Determinare l’espressione vettoriale del momento angolare del ciclista
rispetto all’osservatore quando è nella posizione P2
servendosi del riferimento cartesiano ortogonale illustrato nella figura ed
assumendo come terzo asse cartesiano quello perpendicolare al piano del foglio
ed uscente da questo.
1.4)
Indicare come si esegue analiticamente l’operazione di prodotto
vettoriale tra il vettore posizione OP2 ed il vettore quantità di
moto del ciclista nella posizione P2.
1.5)
Siano A,B,C,D quattro successive posizioni occupate dal ciclista
rispettivamente negli istanti tA, tB, tC, tD
. Nell’ipotesi che gli intervalli di tempo [tA; tB], [tC;
tD] abbiano la stessa durata , determinare le aree dei triangoli OAB,
OCD, essendo O la posizione dell’osservatore ( origine di riferimento degli
assi cartesiani).
| Soluzione
del problema
1.1
Il
ciclista percorre la strada con velocità costante, quindi risulta
costante la sua quantità di moto
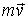. Assunti come puntiformi sia il ciclista che l’osservatore, il momento
angolare del ciclista rispetto all’osservatore, istante per istante, è
dato dal prodotto vettoriale tra il vettore posizione
e la quantità di moto. Ricordiamo ora che il prodotto
vettoriale di due vettori complanari che formino un angolo q,
0£q£p, è un vettore perpendicolare
al piano individuato dai due vettori, con verso dal quale si vede ruotare
il primo vettore in senso antiorario dell’angolo q
per sovrapporsi alla direzione del secondo vettore, modulo pari al
prodotto dei moduli dei due vettori per senq.
Quando
il ciclista è nella posizione P1 l’angolo q formato dal vettore posizione OP1
con il vettore
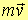è di 90° per cui il momento
angolare ha modulo
|
|
1.2
Quando
il ciclista si trova nella posizione P2, notiamo che con OP2=8m
il triangolo OP1P2 , rettangolo in P1, ha
l’ipotenusa OP2 doppia del
cateto OP1, quindi l’angolo opposto a tale cateto misura 30°.
Indicando allora con
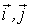
rispettivamente i versori associati agli assi cartesiani x, y
sussiste la seguente espressione analitica per il vettore OP2
:
|
 |
|
1.3
Il
momento angolare del ciclista rispetto all’osservatore, ma rispetto a
qualsiasi altro punto, rimane costante perché risulta costante la sua
quantità di moto; dunque anche quando si trova nella posizione P2
il momento angolare ha modulo
1920Kgm2s-1 .Tenendo
presente le indicazioni del testo, rispetto al riferimento cartesiano Oxyz
indicato, l’espressione del momento angolare è
, essendo
il versore dell’asse
z. |
|
1.4
Dobbiamo
eseguire analiticamente il prodotto vettoriale
.
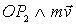Abbiamo già l’espressione vettoriale del vettore
OP2 ; scriviamo ora quella del vettore quantità di moto ed
applichiamo successivamente la regola del determinante per il prodotto
vettoriale. Otterremo il valore indicato nel precedente punto 1.3:
.
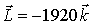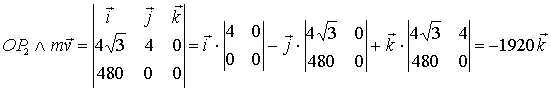
Abbiamo
ottenuto lo stesso risultato. Si noti che il vettore
momento angolare è entrante nel piano del foglio, mentre l’asse
z è uscente.
|
|
1.5
Il
ciclista percorre tratti uguali in tempi uguali perché la sua velocità
è costante. Pertanto la distanza tra le posizioni A
e B è uguale a quella tra le posizioni C e D.
D’altra parte i triangoli OAB , OCD considerati sulle basi AB ,
CD risultano avere uguali le rispettive altezze , che misurano 4m e dunque
le aree degli stessi sono uguali.
In
virtù delle informazioni possiamo perciò scrivere
|
|
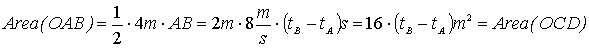
