Torna su

Confronto delle velocità dei tre corpi a fine corsa

    In virtù di quanto visto sulla velocità di caduta per un cilindro pieno, un cilindro cavo e la sfera, quando rotolano giù per un piano inclinato avente altezza h, con velocità iniziali nulle (confrontare discussione_problema_CP, formula (C.15), discussione Cil_c_su_P_inclinato.htm ,Sfera_su_piano_inclinato.htm) possiamo concludere che per i moduli delle rispettive velocità lineari con cui giungono alla base del piano sussiste la seguente catena di disuguaglianze:

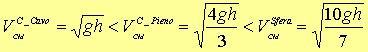
Nota

         Dalla tabella riportata si evince che nelle espressioni delle velocità e dei tempi di caduta non compare la misura del raggio R, ciò implica che se si lasciano rotolare due corpi della stessa forma, che siano omogenei, anche se di materiale diverso, i valori delle suddette grandezze risultano uguali. Ciò è stato verificato in laboratorio lasciando rotolare due sfere, una di legno ed una di acciaio, e due sfere di acciaio aventi raggi diversi.

Confronto tra i tempi di caduta per i tre solidi

Caso della sfera

Le equazioni che descrivono il moto della sfera mentre scende rotolando sono le stesse viste per il cilindro pieno, l’unica differenza sta nel diverso valore per il momento d’inerzia. Riprendiamo dunque quelle equazioni (vedi discussione_problema_CP, secondo metodo).

Mgsenq - F_a=Ma.           (c.6)

t=Ia                              (c.7)

Il momento d’inerzia della sfera rispetto ad un suo qualsiasi asse baricentrale è

  . 

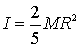Dal valore del momento della forza di attrito rispetto al centro della sfera  t=F_aR ricaviamo

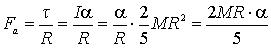
ed ancora dal legame tra accelerazione angolare ed accelerazione lineare per il centro di massa    a=Ra   si deduce

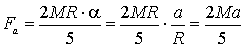                   (s.1)

Sostituiamo questo valore nella (c.6) e ricaviamo successivamente il valore del modulo dell’accelerazione lineare con cui scende il centro della sfera.

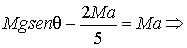
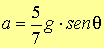                     (s.3)

( Accelerazione di caduta del centro della sfera)

Il moto del centro della sfera è dunque uniformemente accelerato e la sua legge oraria è

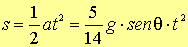                                    (s.4)

        ( Legge oraria del centro della sfera)

Il tempo di caduta della sfera è

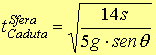                              (s.5)

            (Tempo di caduta per la sfera)

Confrontandolo con il tempo di caduta del cilindro pieno omogeneo avente uguali massa M e raggio R (vedi discussione_problema_CP, secondo metodo, formula (c.14))  quello della sfera risulta inferiore.

Torna su

Caso del Cilindro cavo

         In questo caso il momento d’inerzia rispetto all’asse baricentrale parallelo all’asse di istantanea rotazione è I=MR² . Vogliamo vedere come diventa la forma dell’equazione (c.6) per poter successivamente ricavare l’accelerazione lineare di caduta del centro di massa ed ancora la legge oraria.

Per la forza di attrito si ha (vedi discussione_problema_CP, secondo metodo):

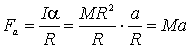,            (CC.1)

per cui l’equazione (c.6) diventa

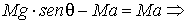
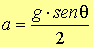                                (CC.2)

                                   (valore dell'accelerazione di caduta)

         L’espressione della legge oraria è dunque

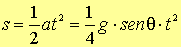         (CC.3)

ed il tempo di caduta è

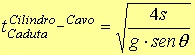       (CC.4)

Confrontando il valore ottenuto con quello del cilindro pieno, 

,

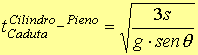 si evince che è maggiore e dunque tra i tre corpi considerati il cilindro cavo è quello che giunge per ultimo alla base del piano; il cilindro cavo è anche quello che immagazzina la maggiore percentuale di energia meccanica sotto forma rotazionale.

 Per i tempi di caduta dei tre corpi sussistono le disuguaglianze: