Momento d’inerzia di una piastra piana rettangolare omogenea di massa M, dimensioni a, b e spessore trascurabile, rispetto all’asse passante per il suo centro di massa (CM) (punto di intersezione delle diagonali del rettangolo) e perpendicolare al piano della piastra.

Per dimostrare la formula indichiamo con s la densità superficiale di massa e supponiamo di suddividere la superficie della piastra in tante strisce sottilissime parallele ai lati di misura a. Ciascuna di tali strisce avrà distanza x dal punto O, centro di massa della piastra, coincidente con il punto di intersezione delle diagonali giacché la piastra è supposta omogenea. Indichiamo con dx la larghezza infinitesima di una delle suddette strisce; l’area sarà ds=a×dx  e la massa elementare compresa nella striscia è

.

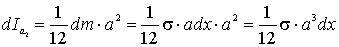Possiamo determinare il momento d’inerzia della striscia rispetto all’asse a₁ applicando il teorema di Steiner. Infatti,  si può determinare prima il suo momento d’inerzia rispetto all’asse baricentrale a₂ parallelo all’asse a₁ e successivamente con il suddetto teorema trovare quello rispetto al punto O.

Il momento d’inerzia della striscia elementare di massa dm rispetto all’asse a₂ per o’ (vedi figura) è^([1])

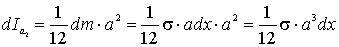
e dunque, applicando il teorema di Steiner, il momento d’inerzia della stessa striscia rispetto all’asse baricentrale a₁ è

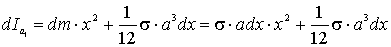
Il momento d’inerzia dell’intera piastra si ricava eseguendo l’integrale definito

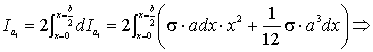
In definitiva, ricordando che per la massa della piastra risulta 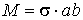, per il momento d’inerzia otteniamo l’espressione

                                  C.V.D.
torna su