T_cilindro

[ Home ] [ Su ] [ Cilindro pieno su piano inclinato ]

Cilindro pieno omogeneo di massa M e raggio r
Premessa
Il lavoro fatto per il calcolo del momento d’inerzia per un disco omogeneo si rivela utile per determinare il momento d’inerzia di un cilindro omogeneo pieno di raggio r rispetto all’asse baricentrale e parallelo alle generatrici della superficie cilindrica. Possiamo, infatti, supporre di sezionare il cilindro con infiniti piani paralleli tra loro e perpendicolari all’asse baricentrale scelto ed ottenere tanti dischi omogenei di cui determinare il momento d’inerzia per poi sommarli per avere il momento d’inerzia dell’intero cilindro. La formula relativa è quindi un’estensione della (8). Qui vogliamo offrire un’opportunità diversa e conseguire il risultato facendo riferimento a cilindri elementari cavi coassiali e sfruttare la formula (9).

Vogliamo dimostrare che per un cilindro omogeneo pieno di raggio r, altezza h e massa M, il momento d’inerzia rispetto ad un asse baricentrale e parallelo alle generatrici della superficie cilindrica che delimita il solido è dato da

(10)

Dimostrazione

Il cilindro può essere pensato come l’unione di infiniti cilindri coassiali di spessore infinitesimo, cioè praticamente formato da infiniti cilindri cavi (vedi figura). In effetti, possiamo considerare il cilindro coassiale alla superficie cilindrica che delimita il cilindro assegnato avente raggio x e spessore dx, con 0£x£ r. Se r è la densità del materiale di cui è composto il solido allora la massa dm corrispondente a detto cilindro elementare è

(10.1)

ed il suo momento d’inerzia dI rispetto all’asse fissato lo si deduce dalla (9), quindi

(10.2)

Il momento d’inerzia dell’intero cilindro pieno si ottiene ancora con un’operazione integrale, precisamente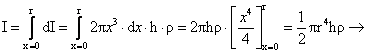

C.V.D.