Consideriamo ora un disco omogeneo di massa M, raggio r e spessore trascurabile. Il suo baricentro coincide con il centro del disco.

Vogliamo dimostrare che il momento d’inerzia rispetto ad un asse baricentrale perpendicolare al piano del disco è

              (8)

 Per dimostrare la formula (8) pensiamo al disco come costituito da tanti anelli sottili concentrici  aventi il centro coincidente con il centro del disco ed indichiamo con s la densità superficiale del disco definita da

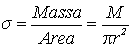          (8.1)

Il generico anello avrà raggio x, con 0£x£ r; indichiamo con   dx  la larghezza della striscia dell'anello. Con detti simboli  l’area ricoperta dalla superficie dell’anello è

ds=2pxdx              (8.2)

 alla quale corrisponde la massa

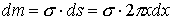.   (8.3)

In virtù  della formula per il momento d’inerzia di un anello omogeneo ideale rispetto ad un asse baricentrale perpendicolare al piano dell'anello, il momento d'inerzia di questo anello, che indichiamo con   dI , è

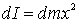                                     (8.4)

Possiamo determinare il momento d’inerzia dell’intero disco eseguendo la somma dei contributi dI   dei singoli anelli. Operativamente si deve calcolare l’integrale definito che segue:

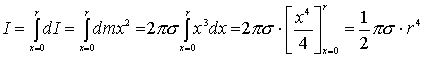
Tenendo ora conto che per la (8.1) si ha M=spr²  segue

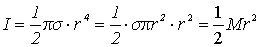                    C.V.D.