
Osserviamo
subito che la massa non scende liberamente perché sulla stessa agisce la forza
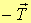 dovuta alla reazione del disco di
massa M che è accelerato proprio dalla massa m
che scende per effetto della sua forza peso. Assumendo
come asse per la descrizione del moto per la massa m
quello verticale passante per il baricentro di questa ed orientato verso il
basso, la seconda equazione della dinamica in forma scalare risulta:
dovuta alla reazione del disco di
massa M che è accelerato proprio dalla massa m
che scende per effetto della sua forza peso. Assumendo
come asse per la descrizione del moto per la massa m
quello verticale passante per il baricentro di questa ed orientato verso il
basso, la seconda equazione della dinamica in forma scalare risulta:
mg-T=ma,
(4.1)
avendo
indicato con a l’accelerazione
della massa.
Notiamo
ora che l’accelerazione con cui scende la massa m
è uguale all’accelerazione tangenziale at
di un qualsiasi punto del bordo disco e che sussistono tra le diverse grandezze
le seguenti relazioni
t=Ia=TR,
at=Ra
Con
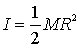
ricaviamo dunque
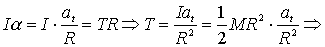
 (4.2)
(4.2)
Sostituendo
nell’equazione (4.1) at
con a si ricava l’espressione
dell’accelerazione con cui scende la massa m.
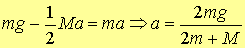 (4.3)
(4.3)
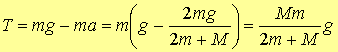 (4.4)
(4.4)
Calcolo
della velocità della massa m
dopo un tratto di discesa Dh
Il
moto di caduta della massa m avviene con
accelerazione uniforme di valore

e
poiché parte da ferma dopo aver
percorso un tratto Dh
avrà acquistato la velocità
Vf data
da
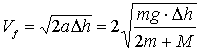 (4.5)
(4.5)
Verifica
del bilancio energetico
Durante
la discesa della massa m quest’ultima perde progressivamente energia
potenziale gravitazionale mentre acquista energia cinetica, ma una parte
dell’energia meccanica gravitazionale perduta è immagazzinata dal disco
rotante sotto forma d’energia di rotazione. Pertanto in un qualsiasi istante
dovrà risultare

Facciamo notare che la
velocità Vf acquistata dalla massa m
è anche quella periferica di un qualsiasi punto del bordo del disco e d’altro
canto, essendo wf la velocità
angolare del disco nello stesso istante, risulta anche
Vf=Rwf.
L’energia cinetica di rotazione del
disco è allora
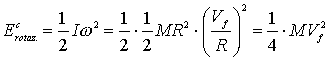
Utilizzando
per Vf l’espressione (4.5) possiamo scrivere diversamente
l’espressione dell’energia cinetica del sistema dopo che la massa m ha
percorso il tratto Dh.
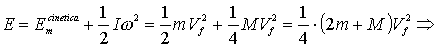
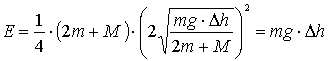
A
questo punto facciamo notare che la diminuzione d’energia potenziale
gravitazionale della massa m quando scende di un
dislivello Dh è proprio il
valore mgDh e dunque abbiamo
trovato che l’energia cinetica totale del sistema delle due masse uguaglia
tale valore. Il bilancio energetico è così verificato.

Applicazione
Supponiamo
che risulti:
M=500g,
m=100g, Dh=50cm,
R=10cm. Trovare la tensione T
del filo e la velocità finale della massa m.
L’accelerazione
di discesa è
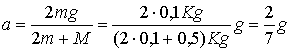
Energia
cinetica della massa m.
Energia cinetica di rotazione
Momento
di’inerzia
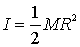
Energia
cinetica di rotazione

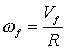 Þ
Þ

Energia
gravitazionale persa dalla massa m

Bilancio energetico
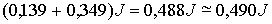 C.V.D.
C.V.D.
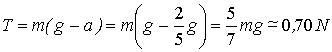

Torna su