Problema - Un pendolo fisico è costituito da un’asticella omogenea di lunghezza 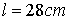e massa M incernierata in suo estremo nel punto O. All’altro estremo è fissato un disco omogeneo di massa M, raggio 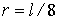, con l’estremo della barretta coincidente con il centro C del disco; il piano del disco è quello verticale in cui oscilla insieme alla barretta.
a)  Determinare il periodo d’oscillazione del pendolo.
b)  Nell’ipotesi che un orologio a pendolo funzioni con il meccanismo indicato, valutare l’eventuale errore nelle 24 ore di un giorno.

Problema- Un’asta rigida AB di lunghezza L e massa M, può ruotare in un piano verticale intorno al suo estremo A vincolato tramite un perno ad un supporto e reca all’estremità libera un altro corpo C₁ di massa M. L’asta è mantenuta in equilibrio in posizione orizzontale tramite un filo, come indicato in figura. Lasciata libera ruota senza attrito e giunta in posizione verticale urta elasticamente un secondo corpo C₂ avente ancora massa M. Determinare:
 1)  La velocità angolare dell’asta immediatamente prima di urtare il corpo C_{2 .}
2)  La velocità angolare dell’asta dopo l’urto e la velocità con cui parte il corpo C₂.

Problema - Un’asta rigida AB di lunghezza L e massa M, può ruotare in un piano verticale intorno al suo estremo A vincolato tramite un perno ad un supporto. All’estremità B libera ed al centro O sono bloccate altre due masse di intensità M/2. L’asta è mantenuta in equilibrio in posizione orizzontale tramite un filo, come indicato in figura. Lasciata libera ruota senza attrito. Determinare la velocità angolare dell’asta e la velocità del centro di massa del sistema meccanico quando la direzione dell’asta forma con la verticale per A un angolo q  

Problema-Una piattaforma circolare di massa M e raggio R ruota senza attrito intorno ad un asse passante per il suo centro O in un piano orizzontale con velocità angolare . Un uomo di massa m si trova nel centro della piattaforma e ad un certo punto comincia a muoversi radialmente dirigendosi verso il bordo della piattaforma. Arrivato sul bordo comincia a correre con velocità 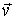in verso opposto a quello nel quale ruota la piattaforma ed il modulo della velocità è tale che l'uomo risulta fermo rispetto al suolo. Risolvere i seguenti quesiti:
1) Determinare il momento angolare e l’energia meccanica del sistema uomo+piattaforma quando l’uomo è collocato nel centro O.
2)  Determinare la velocità angolare con cui ruota il sistema uomo+piattaforma, nonché l’energia meccanica, nell’istante in cui l’uomo raggiunge la posizione estrema sul bordo.
3)  Determinare la velocità angolare della piattaforma, la velocità dell’uomo rispetto alla piattaforma e l’energia cinetica del sistema rotante mentre l’uomo corre sul bordo della piattaforma.
Determinare i valori richiesti delle grandezze nel caso particolare in cui M=180 Kg, m=70Kg, w₀=20giri/min

1)       Il momento angolare del ciclista rispetto all’osservatore nell’istante in cui gli passa davanti      ( Posizione P₁).

2)        Le componenti cartesiane del vettore posizione del ciclista rispetto all’osservatore nel momento in cui il ciclista si trova ad 8m di distanza da O (Posizione P₂). Considerare il ciclista come puntiforme.

3)      Determinare l’espressione vettoriale del momento angolare del ciclista rispetto all’osservatore quando è nella posizione P2 servendosi del riferimento cartesiano ortogonale illustrato nella figura ed assumendo come terzo asse cartesiano quello perpendicolare al piano del foglio ed uscente da questo.

4)        Indicare come si esegue analiticamente l’operazione di prodotto vettoriale tra il vettore posizione OP₂ ed il vettore quantità di moto del ciclista nella posizione P₂.

5)          Siano A,B,C,D quattro successive posizioni occupate dal ciclista rispettivamente negli istanti t_A, t_B, t_C, t_D . Nell’ipotesi che gli intervalli di tempo [t_A; t_B], [t_C; t_D] abbiano la stessa durata , determinare le aree dei triangoli OAB, OCD, essendo O la posizione dell’osservatore ( origine di riferimento degli assi cartesiani).